社団法人 日本測量協会 計算式集 P.238 2.3.6 方向角の計算(取付観測がない場合)
を参考にしたプログラムです。無方向トラバースと呼ぶのが一般的なようです。
この処理方法には賛否があるようですが、TSの距離・角度の測定精度が半世紀前と比べれば飛躍的に向上している現在では、かつての閉合誤差配分より優れていると思います。
取付角の観測が不要なのでTSのセット回数も2箇所減らせますし、取付点の座標精度に影響されることもありません。始終点の座標精度さえ良ければ求点座標も高精度です。
観測数が多いほど精度が上がると主張される方もいらっしゃいますが、それは取付点の座標値が起終点と同じ精度を持っているときだけです。
なお、この手法は公共測量の「基準点測量」には利用できませんが、GioLine pro の利用者様が基準点測量を実施する機会はないでしょう。1級のTSで観測したからといって、成果品が1級基準点にはなりません。
以下の説明は、GioLine pro のユーザ様への計算方法の解説です。
解説内容にはソフト開発者の「主観的」な判断(計算手法)が含まれています。
教科書ではないので、あくまで参考としてお読みください。
また、ユーザ様以外の方は印刷をご遠慮ください。
- 上記計算式集の「 2.3.6 方向角の計算」を参考にしています 下図追加 2025/08/06
- 出発点・結合点での取付角の観測は不要です
- 出発点・結合点は 点番or点名 で指定してください(座標値の直接入力はできません)
- 角度の閉合差の配分はありません(計算手法のため)
- 座標の閉合差の配分は、均等・コンパス・トランシット の3種から選択します
- 投影・縮尺補正に対応しています
- 計算処理の過程でmm丸め等はおこなわず、フル桁で処理しています
Ver.7.240 で 3D(斜距離・高度角)入力、Z値出力に対応しました 詳細はこちら
- 上記計算式集の「 2.3.6 方向角の計算」を参考にしています 下図追加 2025/08/06
使い方
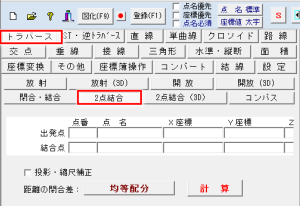
- 出発点 T1 (1000, 800)
- 結合点 T2 (1100,1200)
- P1,P2 が求点です (P1(900,900)P2(800, 1100))
- 入力データ(観測データ)は
1:T1 – P1 の水平距離(141.421m)
2:T1-P1-P2 の水平角(時計回り:161-33-54)と水平距離(223.607m)
3:P1-P2-T1 の水平角(時計回り: 81-52-12)と水平距離(316.228m)
上記の水平角、水平距離は観測に誤差がなかった場合の確定値です。
このまま入力すると誤差無しで座標値が得られます。 - 黒線が現地の辺です(グリッド間隔100m)
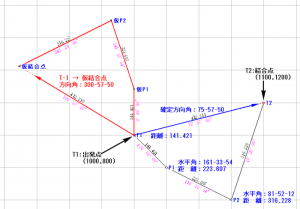
入力画面
水平角・水平距離に多少誤差を与えた数値を入力しています
方向点(後視点)でTSの水平角をゼロセットして得られた水平角です
誤差確認画面
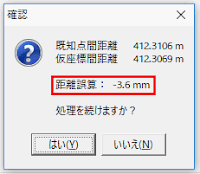
[計算]をクリックすると距離の閉合差(赤枠内 mm 単位)を表示し、継続するか問われます。
ここの数値は観測精度の確認に重要です。通常の結合トラバースでは角度の閉合差と距離(経緯距)の閉合差が出力され、その数値で観測の妥当性を判断しますが、この計算手法では「距離」の閉合差でしか確認ができません。ただし、水平角・距離の誤測や入力ミスがあると誤差が非常に大きくなります。測量の測線長・測点数・TSの精度にもよりますが、誤差が100mmを超えた時は再測が必要かもしれません。
なお、閉合差が1mを越えた時は計算を継続できません(1mは大きすぎますが・・・)
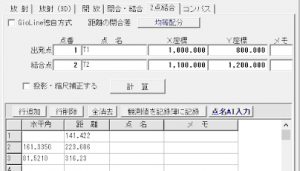
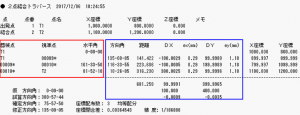
計算結果 1
記録簿へ計算書が出力されます(距離補正:無し 閉合差配分:均等配分)
・赤枠内が入力データ
・青枠内の距離以外の数値はフル桁計算値を出力桁数に丸めています。したがって、出力数値を手計算で合計しても数値が一致しないことがあります。
計算結果 2
距離 補正:あり 計算書の平面距離はフル桁計算です
閉合差配分:コンパス法

※架空のデータのため、精度が悪くなっていますが、出力例としてご覧下さい
計算方法
路線図の黒線が実際の位置ですが、T1からP1への方向角が入力されていないため、通常の結合トラバースとは計算方法が異なります。
1点目(仮P1)の座標は、T1 からの方向角が 0-00-00 と仮定して計算します。
したがって、
X = T1 の X座標 + (T1→P1 の水平距離)= 1000 + 141.422 = 1141.422
Y = T1 の Y座標 = 800.000
とします。
2点目(仮P2)3点目(仮結合点)は水平角が指定されているので、それぞれの座標値を求めることができます。
T1 ー 仮P1 ー 仮P2 ー 仮結合点 は路線図の赤線になり、正しい位置(黒線)にはなりません。
路線図に示したように、赤線を T1 を中心に右回転すれば黒線と「一致」させることができます。
回転角 = 確定方向角(T1 → T2)ー 仮方向角(T1 → 仮結合点) ※下記の数値は上記の計算例のデータとは異なります
= 75-57-50 ー 300-57-50
= – 225-00-00 + 360 (マイナスなので360度を足す)
= 135-00-00
0-00-00 と仮定した方向角を 135-00-00 に修正して再計算すれば、仮方向角(T1 → 仮結合点)とT1 → T2(結合点)方向角を一致させることができます。
したがって、始終点で取付方向角を観測する結合トラバースと違い、角度の閉合差を配分する処理はありません。
仮P1 等を回転させることで、T1 → 仮結合点とT1 → T2 の方向角は一致しますが、仮結合点とT2 の座標値は通常同じ値にならず、閉合差が生じます。閉合差は結合トラバースと同じく、均等・コンパス・トランシット法で配分します
フル桁計算とは
結合トラバース等で角度・座標閉合差は、均等・コンパス・トランシット法 で配分しますが、「慣例」で、
・角度:秒単位(この2点結合トラバースでは角度調整はありません)
・座標:mm単位
共に整数値で配分します。この整数値による配分は処理が面倒な割にメリットを感じられません。
例えば、コンパス法では辺長に比例して座標の閉合差を配分しますが、辺長が 100.000m 100.001m と1mmしか違わなくても 1mm 長い辺へ1mm 配分されます。0.5mm 単位で2点へ配分されることはありません。
座標値が1mm単位との決まりがあるのでmm単位で配分するということなのでしょうが、パソコンで計算する時代に整数値にこだわる理由はあるのでしょうか?
今回追加した 2点結合トラバースでは、上記のような整数値による補正ではなく、補正値は内部演算の有効桁で計算しています。
例:配布数が3点で、閉合差が4ミリ(実際の処理では、閉合差もフル桁で整数値にはなりません)、辺長が同じ時、コンパス法で配分すると、
・従前の配布:1,1,2 or 1,2,1 等
・フル桁配布:4/3,4/3,4/3 (1.33333‥)
となります。
したがって、従前の方法で辺長が短く配布量が0になる場合でもフル桁配布では極小値でも配布されます。
また、計算過程も補正後の座標値はmm単位ではなくフル桁になっていますが、登録時にmm単位に丸められます。
その他のフル桁計算部分
・仮点(仮P1〜仮結合点)座標値
・回転角(10進度)
・DX,DY
・εx,εy
・平面距離 (距離×投影補正×縮尺補正)
メーカー製のソフトの中には
球面距離=距離×投影補正 (mm単位に丸める)
平面距離=球面距離×縮尺補正 (mm単位に丸める)
と2回丸め処理をしているものもあります。
この処理方法に違和感を感じられる方も多いと思いますが、参考にした計算式集には配分方法の説明は一切無く、トランシット法といった用語さえ載っていません。
誤差配分の「決まり」をご存じの方は是非ご教授をお願いします。
その他の注意点
始終点は点番か点名で指定してください(座標値の直接入力は使えません)
座標簿の上にある「計算値登録」がチェックされていなくても常に座標登録されます
結合トラバース計算と共通しますが、新点間距離はほぼ同程度に、新点は10点以下で計画しましょう
閉合・結合トラバースと異なり、測角のミスは「確認」できません。必ず距離の閉合差を確認してください。閉合差が100mmを超えた場合は誤測の可能性があります。
結合トラバースのデータをお持ちなら
手元に結合トラバースのデータ(観測値と計算書)をお持ちなら、そのデータを「2点結合トラバース」で計算し、「結合」との座標差を確認できます。観測が正確なら座標値に大きな違いが無いことをご確認いただけるはずです。
開発者の感想
トータルステーションの登場で半世紀前とは比べものにならない精度で距離・角度の観測が可能になりました。三角測量はもはや死語で基準点測量もGPSが主流です。測量の世界は様変わりで、かなり前に大学の土木系でも測量は必修科目から外されました。
測量器機の飛躍的な精度アップにもかかわらず、いまだに対回観測を求められているのは不思議に感じます。
測量を生業としている方が、対回観測で20秒読みのTSで1秒まで計測できると主張されていて驚いたことがあります。
2点結合トラバースでは取付の観測が不要なため、TSの設置数を2回減らせ、取付点へのターゲットの設置も不要で大幅な時間短縮をはかれます。
しかし、精度が悪いから使ってはいけないと主張される方は珍しくありません。何を根拠に精度が悪いと言われているのか分かりません。従前の結合トラバースでは既知点が4点必要です。その4点の座標精度が極めて良ければ、4点使おうが、そのうちの2点を使おうが結果は同じですし、むしろ観測数が少ない方が精度を期待できます。
確たる根拠もなく、無方向トラバースは精度が悪いと判断(主張)しないでいただきたいものです。
補足 対回観測は昔(戦前)の経緯儀の望遠鏡が長すぎて、今のように同軸に置けず、水平回転軸から偏心してセットされていたためと、当時の角測定は金属板に刻まれた分度盤をバーニヤやマイクロメータで読んでいたため、分度盤の全周360度を使って分度目盛りの刻印誤差を消去するのが目的でした。したがって24対回なども普通におこなわれていたそうです。参考サイト
しかし、現在のTSの望遠鏡は同軸ですし、「分度盤」は半導体製造技術で製造された微細なパターンを光学的に読み取っているので対回で消せる誤差は存在しないと思います。違いますか? (ネットでは分度盤の偏心を除去するため、と解説されている方もいらっしゃいますが、分度盤の偏心は対回で消せるのでしょうか?)
応 用 例
※ 以下の説明は、任意座標系(現場独自の座標系)が前提で、精度については「考慮」していません。
測量範囲が狭ければ放射だけで済みますが、障害物などで視準できない場合は器械を設置する座標点が必要です。もちろん、放射で求めた2点を器械点と方向点にしても構いませんが、2点結合トラバースを使えば、観測精度の確認ができます。
結合・閉合トラバースも結合点(閉合では始点)での閉合差(角度・座標差)で観測精度の確認ができ、それが結合・閉合トラバースを実施する理由の一つです。閉合差の誤差配分の前に、閉合差が基準値以内か確認する必要があります。基準値は発注機関が定めています。
閉合トラバースでは既知点が2点(始点・始点からの方向点)、結合トラバースでは4点(始終点2点+各方向点)が必要です。
工事などで測量を実施した機関から既知点座標を提供されている場合は、その中の座標点を使えば問題ありませんが、新たに「基準点」を新設するときは、GPS観測で平面直角座標系で新点を現地に設置するのが今では一般的です(昔のように三角点から網計算で座標値を確定するには多額の経費がかかります)
2点結合トラバースを使えば、測量作業を大幅に省力化できますし、既知点に国土地理院などが設置した基準点を使えれば平面直角座標系で測量ができます(発注者の承認が必要かも)。
ここでは任意座標系(その現場だけの座標系)で放射より確実(観測ミスを発見しやすい)な方法について解説します(説明の必要はないでしょうが)。

上図のA-Bは測量範囲の点で、AからBが見通せ、2点結合はオレンジ色の破線で示したルートとします。
A,B共に座標値が既知なら別に問題はありませんが、未知の時は、
・A座標値(1000,1000)とする(数値は任意です)
・AからBまでの水平距離を精密に観測する
・距離が 123.456m だった時、
B点座標値を(1000,1000+123.456=1123.456)とする(A点の右にある)
この例では、A,B点のX座標値が同じで、B点はA点から右へ 123.456m 移動した点として計算していますが、B点座標をA点の上方向(1123.456,1000)として計算しても問題ありません。
ただし、観測した水平距離を回転させでB点の座標値を求めると三角関数の影響で2点結合トラバースの計算結果が悪くなるので、必ず観測した水平距離を加算してください。
くどいようですが、上記の「手法」は「基準点」がなく、任意座標系での測量が認められていることが前提です。
2023/12/28