編集中 最終更新 2025/12/05 画像は随時追加します
このページの説明は初歩的な内容です。大半のユーザー様はお読みになる必要はありません
測量は点の位置(関係)を確定することが目的です(2次元に限った話です)。
GPSを使えば観測点の経緯度から平面直角座標系の座標値を確定することができますが、機材も高額で観測に時間もかかり、GioLine pro のユーザー様には無縁だと思いますので、TS(トータルステーション)で観測した角度と距離による座標計算に限って解説します。
高価なTSやプリズムを使った観測から求点の座標値を計算しますが、TSは精密な分度器と精密な巻き尺(定規)と同じです。
したがって方眼紙の上に分度器と定規で観測点をプロットするアナログ的な作業をPCで座標値に変換しているだけです。
なお、多少高価なTSには放射・逆放射・その他の基本測量計算プログラムが内蔵されているので、測量ソフトを使わなくても座標値等が得られます。
角度の測定は右回り(時計回り)
取付点(方向点)を視準し、TSの水平角をゼロセットし、TSを時計回りに回転させて求点を視準して水平角を読みます
数十年前のトランシット(経緯儀)にはゼロセットの機能がないため、ゼロセットが可能なTSでもゼロセットせずにお使いになる方がいらっしゃいますが、GioLine proではゼロセットが仕様です。必ず取付点でゼロセットしてください。
牛方のポケットコンパスでは求点を視準したとき、水平分度盤の磁針が示す角度が磁北からの方向角です
放射と逆放射は測量の基本
放射と逆放射は座標計算に必須の知識です。計算の原理は義務教育レベルの数学ですから、できて当然です。
単線路トラバース(GioLine proは単線路トラバースにしか対応していません)は開放・閉合・結合が基本ですが、いずれも放射を連続して観測していくだけで、放射計算ができれば難しくはありません。
方向角の求め方
GioLine pro のST計算で計算できます(ST計算では1点目に入力した座標点が下図のAになります)
方向角は測量座標のX軸(真北:正しい表現ではありません)からの時計回りの夾角です。
下図の線分A-Bの方向角はθa,θb の2種の方向角で表せます。
※ θaをAからの射出方向角、θbをAへの射入方向角と呼ぶことがあるようです
θb=θa + 180° ただし θb >=360°のときは θb = θb – 360°
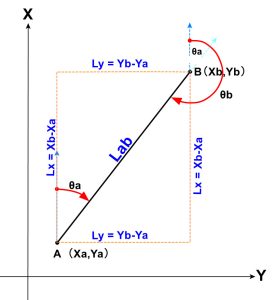
方向角(θa)の計算式
θa = arccos(Lab/Lx) ※測量計算では通常 arctan は使いません
Lab = √(Lx×Lx + Ly×Ly)
Ly = Yb – Ya
ただし Ly < 0 の時は θa = 360°- θa (式の誤りを訂正 2025/07/29)
※ 上記は2点が平面上にある場合であり、球面を考慮する場合は国土地理院の距離と方向角の計算(ST計算)で計算します
方向角による求点座標
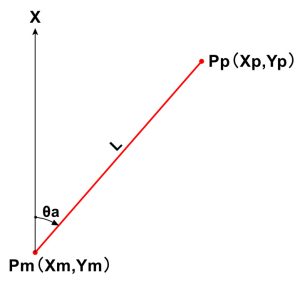
器械点Pm(Xm,Ym)からの方向角(θa)と水平距離(L)が分かれば、求点Pp(Xp,Yp)は、
Xp = Xm + L × cos(θa)
Yp = Ym + L × sin(θa)
で計算できますが、天測や ジャイロ トランシットのような特殊な器機を使わない限り真北(厳密な表現ではありません)を直接知る事はできません。
そこで次の放射(法)のように既知点2点を使って求点方向角を求める必要があります。
放射(法) プログラム、このサイトでは放射トラバースとの誤表記があります
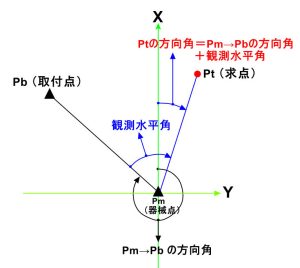
放射(法)では後視点からPt(求点)の夾角(下図では観測水平角)を使って求点の方向角を求めますが、器械点・後視点の座標値が既知であり、現地に杭等が存在している必要があります。
PmとPb(方向点、後視点、取付点等と呼ばれます)の2点の座標値からPm→Pb の方向角を求めます(上記に解説あり)。
Ptの方向角の計算方法は種々ありますが、
Pt の方向角 = Pm→Pb の方向角+観測水平角(夾角)
で計算できます(360°を超えたときは360°減算)
逆放射
文字通り放射の逆ですから、上図のPm、Pb、Pt の全ての座標値が既知です。
放射の式は、
Pt の方向角 = Pm→Pb の方向角+観測水平角(夾角)
です。
逆放射では上式の観測水平角(夾角)を求めたいので、式を変形して
夾角=Ptの方向角 ー(Pm→Pb の方向角) ただし夾角< 0 のときは+360°
距 離
通常TSで観測した斜距離は自動的に水平距離で出力されます。
ただし、距離の定義は厳密には「難しい」です。こちらのサイトの説明が分かりやすいのでご覧ください。
なお、大規模な公共工事の座標系に平面直角座標系が採用されていると思います。
その場合は、平面直角座標系の2点間距離は現地で観測した距離とは一致しません。通常は問題となる「差」は生じませんが、鋼橋等の厳密な寸法を求められる構造物の場合は、必ず現地で補正無しの実寸を確認する必要があります。
蛇足:私は公共工事の座標系に平面直角座標系は必要なのか常々疑問に思っています。高速道路が平面直角座標系で設計されている場合、ジオイド高によっては100mピッチのステーション間の水平距離が現地では100mジャストにはならないはずです。
観測値は丸められている
1秒は意外と小さい
直径100mの円周はπ×100m=3.1415926・・・×100m = 314.1592654・・・mです
360°は 360×60×60 = 1296000秒です
器械点から50m先の1秒は 314.1592654・・・m /1296000 = 0.00024240684m = 0.2424・・・mm です
1秒読みのTSでは 0.2424・・・mm
10秒読みのTSでは 0.2424・・・×10=2.424・・・mm 約2.4mm
したがって50m先のターゲットを1秒読みのTSで視準したとき、ターゲットから0.24mmずれると±1秒の観測誤差が生じます。
10秒読みのTSでも50m先で「許される」視準誤差は2.5mm以下です。
測量を生業とされている方には常識ですが、結合・閉合トラバースに短い辺が含まれると角度の閉合差が大きくなるのは「視準誤差」に影響されるからです。
視準距離が5mの場合、10秒読みのTSでは視準距離50mの1/10の精度で観測する必要があり、2.5mm/10=0.25mmです。0.25mmずれていると10秒違ってしまいます。
当然ですが、TSが基準点上に正確にセットされていない。ターゲットのピンポールが垂直ではない等で観測角の精度はガタ落ちします。
逆に逆放射で杭を設置(測設)する場合、10秒読みTSで50m先では±1.25mm程度の設置誤差が出る可能性があります。
※上記の計算は、微少な tan(θ)≒θ(ラジアン)での近似値です(弦長≒孤長)
1mmは意外と大きい
地球は球体
球の曲率は意外と大きい
水準測量 厳密には難しい
GPSやスマホのレーザー測量(LiDARスキャン)
GPSで平面直角座標系の座標値を求める場合、こちらの動画にもあるように、精度を出すには時間や機材等への投資が必要ですし、国土地理院のサイトに精度は2cm程度と記載されています(もちろん十分に高精度です)。
スマホを使った3D測量の「宣伝」がネット上に多数があり、cm精度を謳っているソフトもありますが、スマホ本体に測定の0位置のマークはありません。
ライカなどの高価な3Dスキャナと解析ソフトを使っても精度1cmを確保することは現状では困難ですし、植生があれば地表は計れません。もちろん災害状況確認(土砂崩れの土量等)には絶大な威力を発揮しますが、公共工事の構造物の施工管理基準を満たすことは困難です。
また、ドローン・解析ソフト・3D_CADを操作できる人材が必要で、継続的な投資が求められます。継続的な受注が見込まれるなら投資する価値はありますが、災害待ちのような不確定要素に「投資」するのは危険だと思います。外注を検討するのが現状では一番安上がりだと私は思います。
今後の技術発展には期待しますがTSが不要になる時代は来るのでしょうか? GPSは元々軍事用で、戦争になれば意図的に誤差信号を出します。
ご参考になれば
・貴重な資料
1980年代にトータルステーションが普及し、それと同時にパソコンも市販されました。当時SEIKOが発売した測量用コンピュータは300万円以上したと記憶しています。TSとPCの普及によって測量業務は一変しましたが、それから40年以上経った現在ではTSもPCも測量ソフト(有名メーカー製)も激安になったと感じています。
私は測量の歴史(技術史・特に機材)に興味があるのでネット等で資料を読むのが楽しみです。特に三角測量にまつわる資料に関心があります。
上西 勝也 先生の「日本測量史」の 明治新政府の測量資料 は先達の業績を知る事ができる大変貴重な資料です(とにかく膨大な情報であたかも「測量の百科全書」)。是非お読みください。
※ 上西先生(博士)は測量史研究家で、英国王立地理学会フェローという大変ご立派な方です。
2025/06/08 恐れ多くも先生からリンクのご許可をいただきました 深謝!
・エベレストの標高
海外の測量ではエベレストの標高を三角測量で求めた「偉業」に感服しました(大三角網)。さすが大英帝国!
詳細はwikiのエベレストをお読みください。以下は要約
1852年当時鎖国状態だったネパールのエベレストの標高を240㎞離れたインドから三角測量で8840mとはじきだしました。現在は8848m前後の標高ですが、170年も前に240㎞かなたから誤差10m以下の精度を出したことには驚くしかありません。
明治期に導入されたカールバンベルヒ社製の経緯儀の水平目盛は0.2秒読み! (2個のバーニヤ読みだったようです)。また、24対回観測も普通だったようです。
分度盤の刻印機をTVで観ましたが(確かミュンヘンの博物館)巨大な機械でした。構造を知りたいのですがネットでは見つかりませんでした。
数表や対数表で計算していた時代の偉業としかいえません。
ご自宅から富士山の剣が峰が見える方はTSで標高を測定してみてはいかがでしょうか?(距離は地図で)
参考「日本測量史」 富士山の測量